はじめに

今回は動的計画法(Dynamic Programming: 通称 DP)の入門記事です。

少し長い記事です。 あと誤字脱字結構あるかもなので変なところあったらｽﾐﾏｾﾝ。🙏

動的計画法とはアルゴリズムの設計技法の 1 つで、深さ優先探索や二分探索などのように細かい手順が定義されたアルゴリズムではなく、よりメタで抽象的な概念になります。今回は DP とはどういうものなのか、その概念に触れてみることが目的の記事になります。

たまたま見つけた中学受験の算数問題に、動的計画法の入門のためとしか思えない良問(?)があったのでそれを例題として進めていきます。👍

注: 興味本位で問題を見てたらあれこれ DP じゃんとなったので題材にしただけで、自分はこれまで中学受験とかそういうのとは全く無縁の人生を送ってきたタイプです。（むしろ学校というものが苦手な人間です。）

問題

図の格子状に引かれた線を道とし、最短距離で点 $A$ から点 $B$ まで移動するとき、考えられる移動経路は全部で何通りありますか。

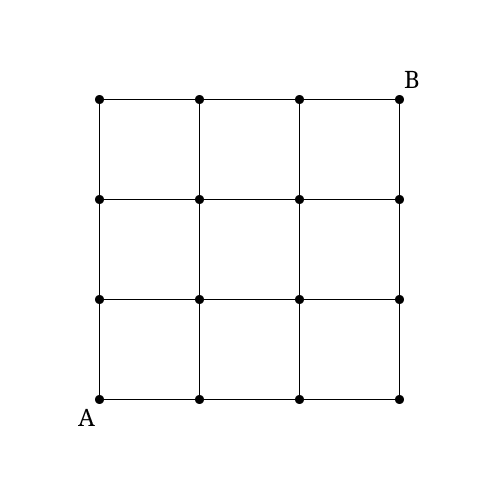
下に考察・解法を書いていきますが、先に進む前によければ問題を解いてみましょう。

考察

説明・考察する際の便宜上、まず格子状の線を座標平面に見立てて、黒い丸がついてる箇所を点、そして点$A$ を $(0, 0)$、点$B$ を $(3, 3)$ と考えて考察していきます。

メモ 点$B$ が $(3, 3)$ だと簡単すぎるかもなので、余裕のある人は点$B$ を $(6, 6)$ として（それにあわせて格子も拡大して）考えてみてください。

最初にどうすれば最短経路になるかを考えます。下または左に進んでしまうと点$B$ から遠ざかってしまうので最短経路にならないとわかります。逆に、右または上方向にのみ進んでいけば最短経路になるとわかります。

なのでここから先は「最短経路になるためには右か上にしか移動できない」ということを前提に進んでいきます。

解法 1

まずもっとも原始的かつ愚直な解法を考えて見ます。

例えば「 $A$ から $B$ までの経路をひたすら全部書いてみる！」という方法はどうでしょうか？

確かに根気さえあればなんとかなるかもしれませんが、ちょっと試してみれば 漏れなくダブりなく 考えられる全パターンの経路を書き出すのはなかなかに難しいことがわかると思います。

点$B$ が $(3, 3)$ くらいであればまだなんとかなるかもしれませんが、これが $(6, 6)$ とかちょっと遠くなっただけで経路数が爆発して手で全列挙するのはほぼ無理になります

そこで、より小さな問題を考えてみます。

点$B$ を $(0, 1)$ としたときの経路は何通りでしょうか？

以下では矢印 $\rightarrow$ で点から点への移動を表現しています

• $(0, 0) → (0, 1)$

の 1 通りしかありませんね。

点$B$ を $(1, 0)$ としたときも同じく 1 通りしかないことがわかります

では、点$B$ を $(1, 1)$ とした場合はどうでしょうか。

• $(0, 0) → (1, 0) → (1, 1)$
• $(0, 0) → (0, 1) → (1, 1)$

の 2 通りだとわかります。

次に $(1, 2)$ までの経路を考えて見ましょう。

上か右にしか移動できないということから $(1, 2)$ の一つ前の点としてあり得るのは $(1, 1)$ と $(0, 2)$ の二つのみとわかります。

$(0, 2)$ の一つ前の点としてあり得るのは $(0, 1)$ のみです。

先ほど $(0, 1)$ までの経路は 1 通りであることを確認しました。ということは $(0, 2)$ までの経路も 1 通りであるとわかります。

そしてすでに $(1, 1)$ までの経路は 2 通りであることを確認しています。

これらの事実から $(1, 2)$ までの経路は $(1, 1)$ までの 2 通りと $(0, 2)$ までの 1 通りを足した 3 通りであるとわかります。

ここまでの考察結果をまとめてみると・・・

上か右にしか移動できないことから、ある点への経路数は、左隣の点への経路数と一個下の点への経路数の和であると一般化できます。

よって点$B$ $(3, 3)$までの経路は $(3, 2)$ までの経路数と $(2, 3)$ までの経路数の和であるとわかります。

ここまで来れば、あとは $(0, 0)$ の経路数を 1 として $(3, 3)$ までを順番に図などに各点の経路数をメモしつつ計算していけば答えを導出できそうですね！

中学受験では図に書き込んでメモしていくというのが 1 つの想定解っぽいですが、実際にそれをやるのはちょっと面倒です。ここでやっとプログラミングを使ってみましょう！

ちなみに今回の考察でやったような、**「ある大きな問題を、同じ形をしたより小さな部分問題に帰着させ、部分問題の計算結果を記録して使い回しながら解いていく」といった手法が動的計画法（Dynamic Programming）**です。

今回くらいの問題だとあまりありがたみがわからないかもしれませんが、部分問題の計算結果を使い回すことで時間計算量を効率化できるところが動的計画法の一つの大きな利点です。

ここまででプログラミングのコードは一切書いてないですが、この解法の考え方は既に動的計画法のそれです。

それでは実際にここまでの考察をコードに落とし込んで行きましょう。

（今回は C++ を使って書いていきます。配列と for がわかれば本質的な部分は読めます。）

コードを書く前にもう一度ポイントをおさらいすると

• ある大きな問題を、同じ形をしたより小さな問題に帰着させ、その小さな問題の解を使って大きな問題を解く
• 分割したより小さな部分問題の解を記録し、再利用することで時間計算量を効率化する

以上が動的計画法のポイントでした。

まず部分問題の計算結果を記録していくことについてですが、これを実現するには俗にいう DP テーブルというもの用意します。今回は考慮すべきパラメーターが $x$ と $y$ の二つあるため、DP テーブルを二次元配列を使って実現します。

そして次に小さな問題の解を使って大きな問題を解くについてですが、まずはコードを書く前に式を考えて見たいと思います。

ここまでで既に、ある点への経路数は、左隣の点への経路数と一個下の点への経路数の和である ことがわかっています。この関係性を使って式を立ててみましょう。

$F(x, y) :=$ 点 $(x, y)$ の経路数

とすると・・・

$F(x, y) = F(x, y - 1) + F(x - 1, y)$

という式が立てられそうです。

ですが、よくよく考えるとこの式は完璧ではありません。

例えば $x = 0, y = 3$ のときに $F(0, 3) = F(0, 2) + F(-1, 3)$ となりますが、$(-1, 3)$ という点は存在しないのでおかしなことになってしまいます。

同じように $y = 0$ のときもおかしくなってしまいます。

というわけでしっかりと場合分けを考慮してもう一度ちゃんと式を立ててみましょう。

こんな感じでしょうか。ちょっと場合分けが多いですね・・・ もうちょっと考えると、$x$ または $y$ が $0$ ならそれより左側または下側どちらか片方にしか点がない、つまり経路が複数になる可能性がないため、 $1$ としてしまっても良いことがわかります。

そうすると下記のように、よりシンプルな式にすることができますね！

あとはこの式で表現される関係をそのままコード化すれば部分問題を使ってより大きな問題を解くといったことが実現できそうです。

ちなみに、このような式を漸化式と呼んだりします。

ところで DP をコード化する際の手法として代表的なものに、配る DP、貰う DP、メモ化再帰（どれも本質的にはほとんど同じです）などがあります。（一部でそう呼ばれるくらいのレベルのもので、何かの正式名称とかではないです。）

配る DP、貰う DP の呼称はこちらの記事より拝借しました。

ざっくり説明すると、

• メモ化再帰は文字通り再帰的に DP テーブルにメモしながら解いていくやり方（すでに DP テーブルに結果がメモされていればその値を使い回す）
• 貰う DP は小さい方から大きい方へ、現在みている部分問題をそれより小さい部分問題の結果を使って解いていくやり方
• 配る DP は小さい方から大きい方へ、現在みている部分問題の結果を部分問題の関係性を利用してより大きいほうへ配りながら解いていくやり方

です。

今回の場合だと、漸化式をそのまま再帰関数で書いてメモ機能を入れつつ実装すればメモ化再帰、ボトムアップなループで下からやっていくような実装をすれば貰う DP になります。

ですが、実は今回の問題では配る DP のほうが簡単にコードが書けるのでそっちでやってみたいと思います。

なぜ配る DP のほうが簡単にコードが書けるのかはいったん置いておいて、実現方法を見ていきましょう。

配る DP で実現する場合、小さい方から順番に、ある部分問題の解 $=$ つまりある点の経路数をより遠い点に配っていきます。

具体的には、点$(x, y)$ の結果を点$(x, y + 1)$ と点$(x + 1, y)$に配ってやれば実現できます。

では実現方法がわかったところで、なぜ今回の問題で配る DP のほうがコードを書くのが簡単なのか考えてみましょう。

メモ化再帰の場合も貰う DP の場合も $x$ または $y$ が 0 以下の場合を考慮する必要があります（再帰の場合はベースケースとして、貰う DP の場合は配列外参照やセグフォを防ぐため）。

ですが配る DP の場合はそもそも大きい方しかみないので $x$ や $y$ が $0$ だったとしてもそれより小さい方を考慮する必要がないことがわかります。（ただし、どんどん大きい方へ配ろうとすることを考えるとテーブルをちょっと大きく持っておく必要がありますが、逆に言うとそれだけで済みます）

では実際にコードを書いて見ましょう。

#include <iostream>
#include <cstring>
using namespace std;

int main() {
  // dpテーブル
  int dp[10][10]; // [10][10]も必要ないですが、余分にとっています

  memset(dp, 0, sizeof(dp)); // 一旦dpテーブルを0で初期化します

  dp[0][0] = 1;

  for (int x = 0; x < 4; x++) {
    for (int y = 0; y < 4; y++) {
      // 「配るDP」
      dp[x + 1][y] += dp[x][y];
      dp[x][y + 1] += dp[x][y];
    }
  }

  cout << dp[3][3] << endl;

  return 0;
}

最初の dp テーブルの初期化時に余分にサイズを大きくとっていますが、それだけです。if 文すら登場しません。

この問題の正解は $20$ ですが、このコードを実行すると正しく $20$ という結果が出力されます。:clap:

自力で解けた方はおめでとうございます！:thumbsup:

ちなみに点$B$ を $(6, 6)$ とした場合の答えは $924$ です。

オマケ（解法 2）

もう一つの解法を見て行きましょう。（こちらの解法は義務教育の範囲をちょっと飛び出して、高校数学の知識を使います。）

ちなみにこちらの解法は DP ではないです。

数学が得意な人は問題を見た瞬間に「パスカルの三角形やんけ！」となったかもしれません。

この手の組み合わせが絡んでくる問題ではパスカルの三角形が潜んでいたりすることがよくあります。めっちゃあります。

そもそもパスカルの三角形って何？な方向けにWikipedia へのリンクを貼っておきます。

ちょっと線を伸ばしてさらに回転させてみるとわかりやすいかもしれません。

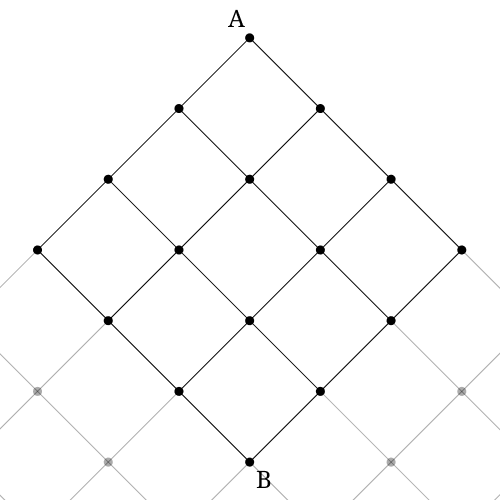
どうでしょう？パスカルの三角形が見えたのではないでしょうか？

パスカルの三角形が見えなかった方は解法 1 の考え方を使って、図の各点に経路数を書き込んでみるとわかると思います。（これをやると答えが求まっちゃいますが・・・）

ということは、

• $(0,0)$ を ${}_0 \mathrm{ C }_0$
• $(1,0)$ を ${}_1 \mathrm{ C }_0$
• $(0,1)$ を ${}_1 \mathrm{ C }_1$
• $(2,0)$ を ${}_2 \mathrm{ C }_0$
• $(1,1)$ を ${}_2 \mathrm{ C }_1$
• $(0,2)$ を ${}_2 \mathrm{ C }_2$

・・・としてコンビネーションを使って各点の経路数を表現することができます。

そうすると点$B$ $(3,3)$ は ${}_6 \mathrm{ C }_3$ だとわかります。

あとはを ${}_6 \mathrm{ C }_3$ を計算するだけです。（プログラミングするまでもないですね 🤣）

以上で $20$ と正しい答えがでて問題を解けました！👏

おわりに

今回の問題は動的計画法としてみるとかなり簡単な問題です。 もっとしっかり勉強してみたいと言う方は こちらの記事 がとてもわかりやすいのでオススメです！